特殊函数.md 3.3 KB
特殊函数
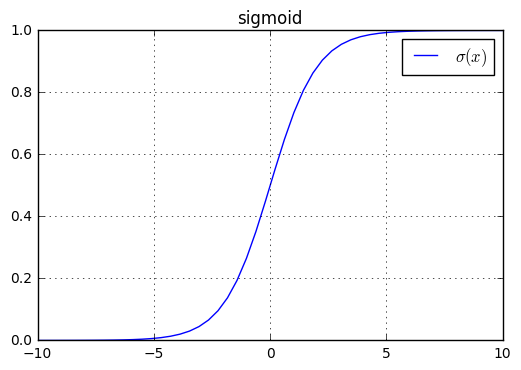
sigmoid 函数
$$ \sigma(x)=\frac{1}{1+\exp (-x)} $$
该函数可以用于生成二项分布的 $\phi$ 参数,当 $x$ 很大或者很小时,该函数处于饱和状态。此时函数的曲线非常平坦,并且自变量的一个较大的变化只能带来函数值的一个微小的变化,即:导数很小。
sigmoid 函数遵循以下性质:
$$ \sigma(x)=\frac{\exp (x)}{\exp (x)+\exp (0)}
\ {\frac{d}{d x} \sigma(x)=\sigma(x)(1-\sigma(x))}
\ {1-\sigma(x)=\sigma(-x)} $$
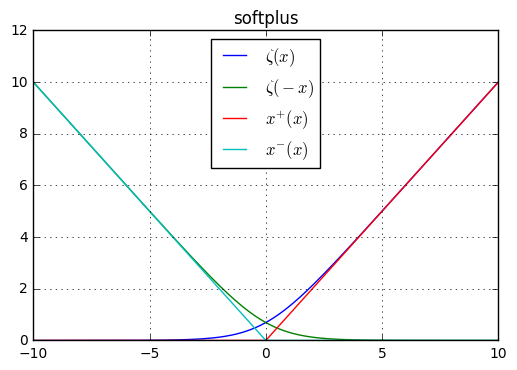
softplus 函数
$$ \zeta(x)=\log (1+\exp (x)) $$
该函数可以生成正态分布的 $\sigma^{2}$ 参数,该函数之所以被称为 softplus,是因为其是 $x^{+}=\max (0, x)$ 函数的光滑逼近:
对于函数 $x^{+}=\max (0, x)$ 以及 $x^{-}=\max (0, -x)$,它们分别获取了 $y=x$ 的正部门和负部分。根据定义有 $x = x^{+} - x^{-}$,而 $\zeta(x)$ 逼近的是 $x^{+}$,$\zeta(-x)$ 逼近的是 $x^{-}$,于是有:
$$ \zeta(x)-\zeta(-x)=x $$
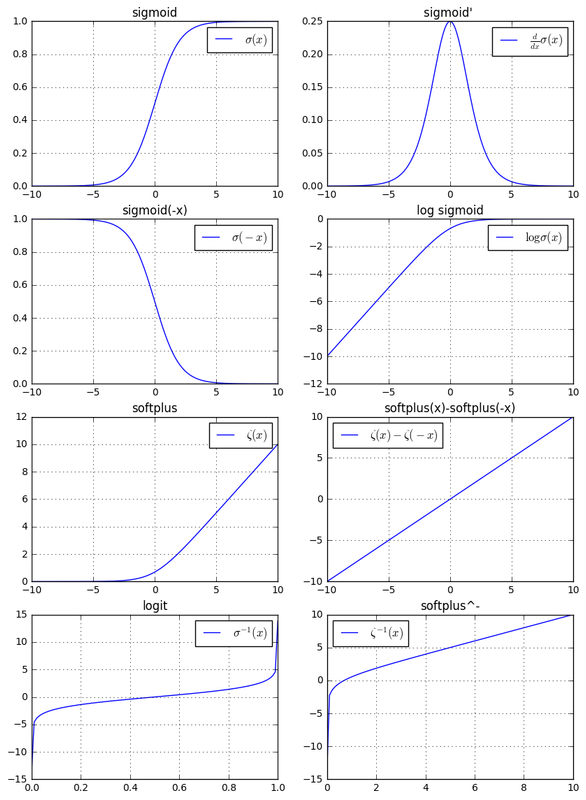
softplus 与 sigmoid 有很多相通的性质:
$$ {\log \sigma(x)=-\zeta(-x)} \ {\frac{d}{d x} \zeta(x)=\sigma(x)} \ {\forall x \in(0,1), \sigma^{-1}(x)=\log \left(\frac{x}{1-x}\right)} \ {\forall x>0, \zeta^{-1}(x)=\log (\exp (x)-1)} \ {\zeta(x)=\int_{-\infty}^{x} \sigma(y) d y} \ {\zeta(x)-\zeta(-x)=x} $$
其中 $f^{-1}(\cdot)$ 为反函数,$\sigma^{-1}(x)$ 也称作 logit 函数:
伽马函数
伽马函数定义为:
$$ \begin{array}{c}{\Gamma(x)=\int{0}^{+\infty} t^{x-1} e^{-t} d t \quad, x \in \mathbb{R}} \ {\text { or. } \quad \Gamma(z)=\int{0}^{+\infty} t^{z-1} e^{-t} d t \quad, z \in \mathbb{Z}}\end{array} $$
$\Gamma$ 函数的性质有:
对于正整数 $n$ 有:$\Gamma(n)=(n-1) !$
$\Gamma(x+1)=x \Gamma(x)$,伽马函数是阶乘在实数域上的扩展。
与 Beta 函数的关系:
$$ B(m, n)=\frac{\Gamma(m) \Gamma(n)}{\Gamma(m+n)} $$
- 对于 $x \in(0,1)$ 有:
$$ \Gamma(1-x) \Gamma(x)=\frac{\pi}{\sin \pi x} $$
即 $\Gamma\left(\frac{1}{2}\right)=\sqrt{\pi}$,当 $x$ 足够大时,可以使用 Stirling 公式来计算 Gamma 函数值:$\Gamma(x) \sim \sqrt{2 \pi} e^{-x} x^{x+1 / 2}$。
Beta 函数
对于任意实数 $m, n>0$,Beta 函数的定义为:
$$ B(m, n)=\int_{0}^{1} x^{m-1}(1-x)^{n-1} d x $$
其他形式的定义还包含:
$$ \begin{array}{c}{B(m, n)=2 \int{0}^{\frac{\pi}{2}} \sin ^{2 m-1}(x) \cos ^{2 n-1}(x) d x} \ {B(m, n)=\int{0}^{+\infty} \frac{x^{m-1}}{(1+x)^{m+n}} d x} \ {B(m, n)=\int_{0}^{1} \frac{x^{m-1}+x^{n-1}}{(1+x)^{m+n}} d x}\end{array} $$
性质
连续性,Beta 函数在定义域 $m, n>0$ 内连续
对称性,$B(m, n)=B(n, m)$
递推公式:
$$ \begin{array}{l}{B(m, n)=\frac{n-1}{m+n-1} B(m, n-1), \quad m>0, n>1} \ {B(m, n)=\frac{m-1}{m+n-1} B(m-1, n), \quad m>1, n>0} \ {B(m, n)=\frac{(m-1)(n-1)}{(m+n-1)(m+n-2)} B(m-1, n-1), \quad m>1, n>1}\end{array} $$
- 当 $m,n$ 较大时,有近似公式:
$$ B(m, n)=\frac{\sqrt{(2 \pi) m^{m-1 / 2} n^{n-1 / 2}}}{(m+n)^{m+n-1 / 2}} $$
- 与 Gamma 函数关系
对于任意正实数 $m, n>0$,有
$$ B(m, n)=\frac{\Gamma(m) \Gamma(n)}{\Gamma(m+n)} $$
且 $B(m, 1-m)=\Gamma(m) \Gamma(1-m)$。