特殊矩阵.md 2.8 KB
特殊矩阵
方阵
方阵的行列式定义如下:
- $1$ 阶方阵的行列式为该元素本身
- $n$ 阶方阵的行列式等于它的任一行或者列的各元素与其对应的代数余子式乘积之和。
稀疏矩阵
对于那些零元素数目远远多于非零元素数目,并且非零元素的分布没有规律的矩阵称为稀疏矩阵(sparse)。人们无法给出稀疏矩阵的确切定义,一般都只是凭个人的直觉来理解这个概念,即矩阵中非零元素的个数远远小于矩阵元素的总数,并且非零元素没有分布规律。
由于稀疏矩阵中非零元素较少,零元素较多,因此可以采用只存储非零元素的方法来进行压缩存储。由于非零元素分布没有任何规律,所以在进行压缩存储的时侯需要存储非零元素值的同时还要存储非零元素在矩阵中的位置,即非零元素所在的行号和列号,也就是在存储某个元素比如 $a_(ij)$ 的值的同时,还需要存储该元素所在的行号 i 和它的列号 j,这样就构成了一个三元组 (i,j,aij) 的线性表。
三元组可以采用顺序表示方法,也可以采用链式表示方法,这样就产生了对稀疏矩阵的不同压缩存储方式。
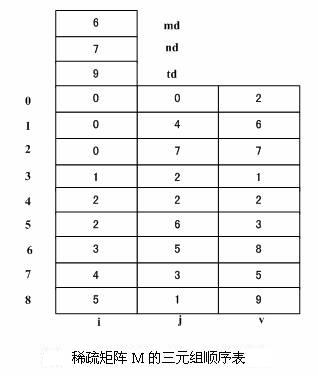
稀疏矩阵的顺序实现
若把稀疏矩阵的三元组线性表按顺序存储结构存储,则称为稀疏矩阵的三元组顺序表。顺序表中除了存储三元组外,还应该存储矩阵行数、列数和总的非零元素数目,这样才能唯一的确定一个矩阵。
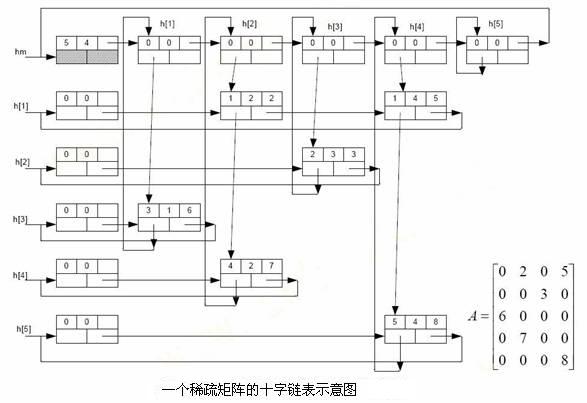
稀疏矩阵的十字链表实现
十字链表结点分为三类:
表结点,它由五个域组成,其中 i 和 j 存储的是结点所在的行和列,right 和 down 存储的是指向十字链表中该结点所有行和列的下一个结点的指针,v 用于存放元素值。
行头和列头结点,这类结点也有域组成,其中行和列的值均为零,没有实际意义,right 和 down 的域用于在行方向和列方向上指向表结点,next 用于指向下一个行或列的表头结点。
总表头结点,这类结点与表头结点的结构和形式一样,只是它的 i 和 j 存放的是矩阵的行和列数。
十字链表可以看作是由各个行链表和列链表共同搭建起来的一个综合链表,每个结点 aij 既是处在第 i 行链表的一个结点,同时也是处在第 j 列链表上的一个结点,就你是处在十字交叉路口上的一个结点一样,这就是十字链表的由来。十字链表中的每一行和每一列链表都是一个循环链表,都有一个表头结点。